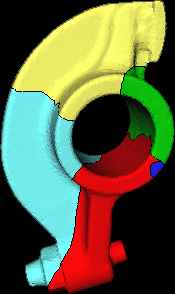
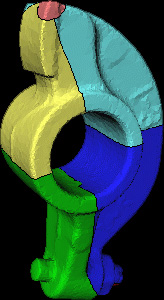
Local parameterization of arbitrary triangle meshes.

We developed a novel approach to the parameterization of triangle meshes representing 2-manifolds with an arbitrary genus. A topology-based decomposition of the shape is computed and used to segment the shape into primitives, which define a chart decomposition of the mesh. Then, each chart is parameterized using an extension of the barycentric coordinates method. The charts are all 0-genus and can be of three types only, depending on the number of boundary components. The chart decomposition and the parameterization are used to define a shape graph where each node represents one primitive and the arcs code the adjacency relationships between the primitives. Conical and cylindrical primitives are coded together with their skeletal lines that are computed from and aligned with their parameterization. The application of the parameterization approach to remeshing guarantees that extraordinary vertices are localized only where two patches share a boundary and they are not scattered on the whole surface.

Patanè G., Spagnuolo M., Falcidieno B. Para-Graph: Graph-Based Parameterization of Triangle Meshes with Arbitrary Genus. In: Computer Graphics Forum, vol. 23 (4) pp. 783-797. Blackwell Publishing, 2004. [PDF]

Global Parameterization of Bordered Triangle meshes with arbitrary genus

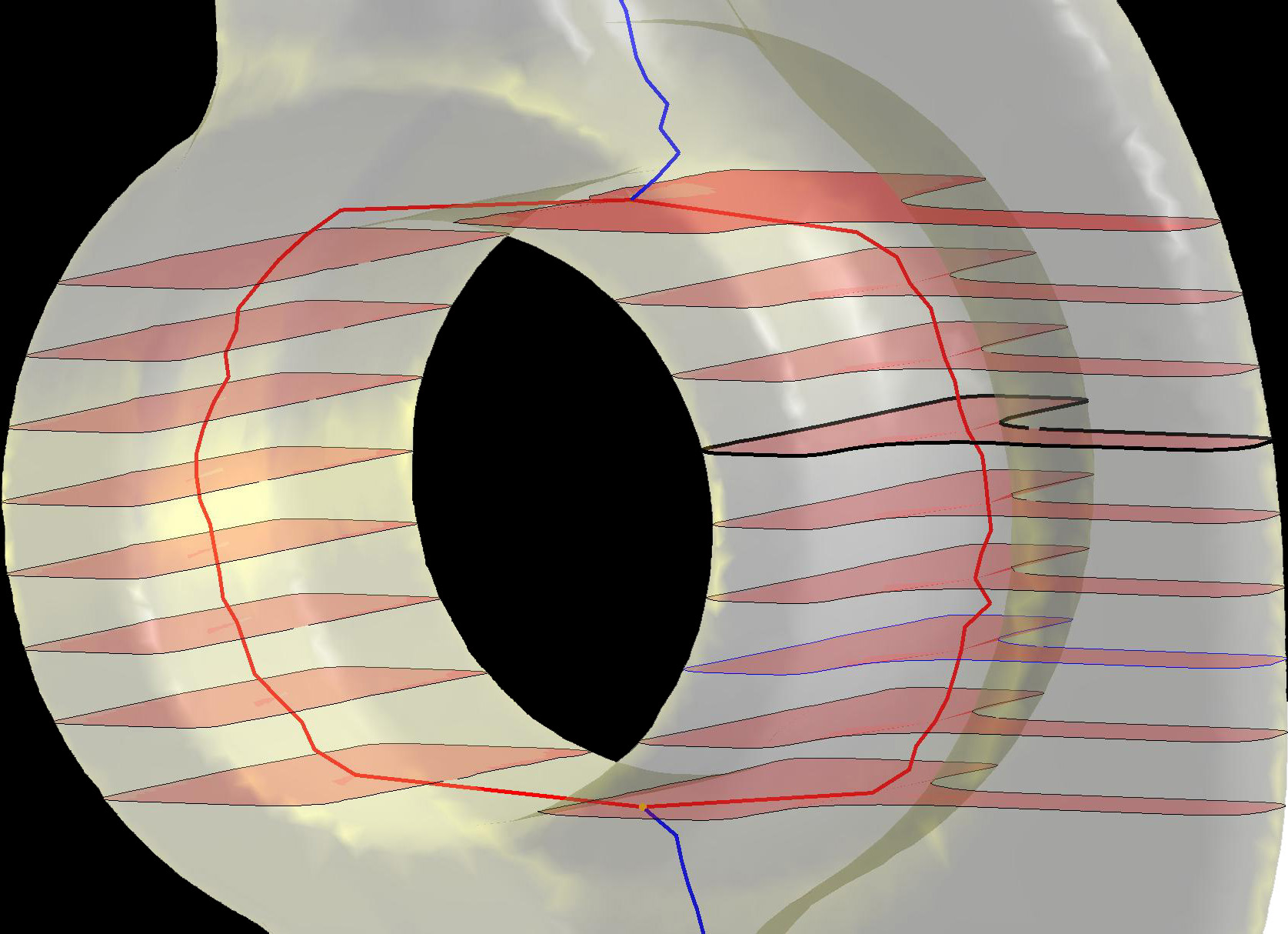
The set of cut graphs for a given triangle mesh M with an arbitrary genus depends on the underlining topology and the selection of a specific one should be guided by the surface geometry and  targeted applications. The influence of the mesh connectivity on the cut graph search affects previous work due to the use of algorithms based on mesh traversal techniques for the evaluation of the geodesic metric. Our solution is to search a cut graph made of the iso-contours of a fair function f: M->R and to work in a planar domain where geodesic curves are defined by line segments whose counterparts on M, with respect to an appropriate diffeomorphism, give smooth approximations of geodesic paths. The emphasis of the paper is on the definition of a simple method for finding a family of cut graphs of M and guided by several criteria which spread from the global parameterization (e.g., minimal length, minimization of the parameterization distortion, or interpolation of points as required by remeshing and texture mapping) to the calculation of polygonal schemes for surface classification. The proposed approach finds a cut graph of a closed or bordered triangle mesh M with n vertices in O(n) time if M has 0-genus, and O(nlog(n)) time if g>0; finally, the associated polygonal schema is reduced if g=0 and with a constant number of redundant edges otherwise.

Patanè G., Spagnuolo M., Falcidieno B. Families of cut-graphs for bordered meshes with arbitrary genus . In: Graphical Modeals, 2006.To appear. [PDF]